遗传算法求解TSP问题的DEAP实现

发表于 更新于 分类于 阅读次数：

用GA求解N个节点的TSP问题，首先导入可能用到的库。

1
2
3
4
5
6
7
8
9
10
# 导入deap相关库
from deap import base
from deap import creator
from deap import tools
from deap import algorithms

import numpy as np
import matplotlib.pyplot as plt
import random
import json

读取数据

输入数据的组织形式根据自己组织，本文从json文件中读取TSP的城市个数和距离矩阵。

1
2
3
4
5
6
# 才能够json文件中读取信息
with open("tsp/gr17.json", "r") as tsp_data:
    tsp = json.load(tsp_data)

distance = tsp['DistanceMatrix']
N = tsp['TourSize']

问题定义

借助DEAP的Creator类可以定义算法需要的类，这些类的基类可以是Python类，如：列表list，集合set，字典dict, 也可以是PrimitiveTree等Deap内建类。基本语法是：

creator.create(name, base[,attribute[,...]])：生成名为name的类，其基类为base，具备属性attribute。示例：

1
creator.create("Foo", list, bar=dict, spam=1)

上述命令定义了一个名为Foo的类，等价于：

1
2
3
4
5
class Foo(list):
    spam = 1

    def __init__(self):
        self.bar = dict()

需要注意的是，尽管基类为numpy.ndarray时定义类没有什么特别需要注意的，但在复制、交叉、变异等算子中进行复制、切片时需要注意，numpy数组的切边是原数组的视图。

对于TSP问题，我们首先定义问题。下面第2行代码定义了一个名为FitnessMin的类，基类为DEAP的base模块中定义的Fitness，属性weights为目标函数的权重元组，负号表明问题为最小化。需要注意的是，weights必须为元组，哪怕为单目标优化，因此后面的逗号一定不能漏掉。

1
2
3
4
# 定义问题
creator.create("FitnessMin", base.Fitness, weights=(-1.0,))
# 定义个体，数据组织形式为list
creator.create("Individual", list, fitness=creator.FitnessMin)

上述代码的第4行，定义了一个Individual类，具有属性fitness。其基类为list，是一个容器类，即我们在后续进化时每个个体都将存储在list中。

初始化

工具箱Toolbox提供了一系列进化算法的算子，譬如克隆函数clone可以复制个体。下面是一些常用的函数：

register函数

register(alias, method[,argument[,...]])在toolbox中注册别名为alias的函数method，如果该函数需要参数可以在注册时一并注册，也可以运行时传入。譬如：

1
2
3
4
5
6
7
8
def func(a, b, c=3):
    print(a, b, c)

# 实例化工具箱
toolbox = base.Toolbox()
# 注册函数myfunc
toolbox.register('myfunc', func, 2)
toolbox.myfunc(b=3)

2 3 3

1
toolbox.myfunc(3,6)

2 3 6

函数注册后如果要修改或重新注册，则必须先解除注册。解除注册函数为unregister(alias)。

染色体定义

TSP问题中，我们采取顺序编码，即列表中城市的编号出现顺序即为访问顺序。该初始顺序的获取可以采用random.sample抽样函数获得，并将其注册为seq函数。

1
2
# random模块的sample函数：random.sample(population, k)
toolbox.register("seq", random.sample, range(N), N)

完成上述注册后可以直接跟普通函数一样使用，从而得到一个初始化序列。

1
2
gen1 = toolbox.seq()
print(gen1)

[4, 10, 5, 1, 3, 7, 12, 8, 15, 14, 6, 0, 11, 13, 9, 16, 2]

常用初始化函数

Deap的tools库提供的常用的初始化方法有：

  1. initRepeat(container, func, n)：调用func函数n次，并将结果放在容器container的一个实例中。容器container可以是列表、数组等Deap支持的容器。例如：

    1
    2
    import random
    tools.initRepeat(list, random.random, 2)

    [0.8225936649126916, 0.6002191666325332]

  2. initIterate(container, generator)：生成器generator返回的结果放在容器container的一个实例中。例如：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    # 菲波拉契数列生成器
    def fib(m):
        n, a, b = 0, 0, 1
        while n < m:
            yield b
            a, b = b, a+b
            n= n + 1

    from functools import partial        
    gen_idx = partial(fib, m=5)  
    a2 = tools.initIterate(list, gen_idx)
    a2

    [1, 1, 2, 3, 5]

  3. initCycle(container, seq_func, n=1)：循环调用函数列表seq_func中的函数n次，并将结果置入容器container中。示例：

    1
    2
    3
    4
    gen_un = partial(random.uniform, 5, 10)
    func_seq = [lambda: 'a' , random.random, gen_un]
    a3 = tools.initCycle(list, func_seq, 3)
    a3

    ['a', 0.8030720384393988, 7.8457022332673265, 'a', 0.5446743044675127, 8.752604169941414, 'a', 0.6014232944342702, 9.736003828310825]

定义个体

TSP问题中，每个个体只有一条染色体。注册个体生成函数individual，内容为调用函数tools.initIterate，两个参数分别为creator.Individual和toolbox.seq。根据前面initIterate介绍，函数individual实际功能就是将seq的结果放在容器Individual中。

1
toolbox.register("individual", tools.initIterate, creator.Individual, toolbox.seq)
1
2
ind1 = toolbox.individual()
print(ind1)

[2, 0, 5, 3, 6, 8, 1, 12, 14, 11, 16, 13, 10, 4, 7, 9, 15]

类似的定义种群函数population

1
2
3
4
5
# 定义种群
toolbox.register("population", tools.initRepeat, list, toolbox.individual)
# 种群规模为5的种群
pop = toolbox.population(5)
print(pop)

[[5, 7, 6, 12, 14, 10, 11, 15, 8, 3, 1, 0, 9, 13, 4, 2, 16], [16, 10, 9, 1, 2, 14, 5, 3, 7, 8, 6, 13, 0, 12, 4, 15, 11], [6, 4, 15, 16, 10, 1, 0, 11, 14, 8, 9, 3, 12, 13, 2, 5, 7], [13, 16, 11, 8, 15, 6, 5, 4, 1, 14, 12, 2, 7, 3, 9, 0, 10], [9, 2, 15, 10, 7, 14, 5, 0, 6, 13, 1, 3, 12, 4, 8, 16, 11]]

定义算子

遗传算法进化过程中需要进行交叉、变异和选择，DEAP内置了很多经典算子，部分如下：

CrossOver Mutation Selection
cxOnePoint() mutGaussian() selTournament()
cxTwoPoint() mutShuffleIndexes() selRoulette()
cxUniform() mutFlipBit() selBest()
cxPartialyMachted() mutUniformInt() selNSGA2()
cxBlend() mutESLogNormal() selNSGA3()

更多内置算子及其用法介绍请参考Deap官方文档。本例中我们直接使用内置的交叉、变异和选择算子。

1
2
3
toolbox.register("mate", tools.cxPartialyMatched)
toolbox.register("mutate", tools.mutShuffleIndexes, indpb=0.05)
toolbox.register("select", tools.selTournament, tournsize=3)

交叉

本例中的交叉算子采用PMX交叉，交叉后返回两个子个体。

1
2
ind1 = toolbox.individual()
ind1

[2, 0, 3, 15, 8, 6, 16, 9, 14, 7, 5, 1, 13, 12, 10, 11, 4]

1
2
ind2 = toolbox.individual()
ind2

[6, 4, 16, 2, 1, 9, 10, 13, 0, 8, 3, 5, 15, 7, 14, 12, 11]

1
2
3
# 克隆ind1，ind2
child1, child2 = [toolbox.clone(ind) for ind in (ind1, ind2)] 
child1

[2, 0, 3, 15, 8, 6, 16, 9, 14, 7, 5, 1, 13, 12, 10, 11, 4]

1
child2

[6, 4, 16, 2, 1, 9, 10, 13, 0, 8, 3, 5, 15, 7, 14, 12, 11]

对child1和child2进行交叉：

1
toolbox.mate(child1, child2)

([15, 4, 16, 6, 1, 9, 10, 2, 14, 7, 5, 8, 13, 12, 3, 11, 0], [9, 0, 10, 15, 8, 2, 3, 13, 4, 1, 16, 5, 6, 7, 14, 12, 11])

变异

变异采用随机排序（shuffle）变异。

1
2
mutant = toolbox.clone(ind1)
mutant

[2, 0, 3, 15, 8, 6, 16, 9, 14, 7, 5, 1, 13, 12, 10, 11, 4]

1
toolbox.mutate(mutant)

([2, 0, 3, 15, 8, 6, 16, 9, 14, 7, 10, 1, 13, 12, 5, 11, 4],)

选择

适应度计算

首先定义适应度计算函数。

1
2
3
4
5
6
7
8
9
10
# 定义适应度计算函数
def evalTSP(ind):
    fit = distance[ind[-1]][ind[0]] # 最后一个节点到第一个节点的距离
    for o, d in zip(ind[0:-1], ind[1:]):
        fit += distance[o][d]
    
    return fit,

# 注册适应度函数
toolbox.register("evaluate", evalTSP)

回顾之前定义，每个个体都有一个名为fitness的属性，我们可以判断一个个体的属性值是否合法。

1
2
# 判断适应度值是否合法（是否已经计算）
ind1.fitness.valid

False

对个体进行评估，并把评估函数返回值赋值给fitness的values属性。

1
2
3
ind1.fitness.values = toolbox.evaluate(ind1)
# 查看适应度值
ind1.fitness.values
(4288.0,)

此时在判断适fitness是否合法：

1
ind1.fitness.valid

True

对于整个种群的个体进行适应度值计算，并赋值：

1
2
3
# 计算种群pop的适应值函数
fitnesses = list(map(toolbox.evaluate, pop))
fitnesses

[(4145,), (3716,), (4915,), (4173,), (5147,)]

1
2
3
4
for ind,fit in zip(pop, fitnesses):
    ind.fitness.values = fit
    
pop

[[5, 7, 6, 12, 14, 10, 11, 15, 8, 3, 1, 0, 9, 13, 4, 2, 16], [16, 10, 9, 1, 2, 14, 5, 3, 7, 8, 6, 13, 0, 12, 4, 15, 11], [6, 4, 15, 16, 10, 1, 0, 11, 14, 8, 9, 3, 12, 13, 2, 5, 7], [13, 16, 11, 8, 15, 6, 5, 4, 1, 14, 12, 2, 7, 3, 9, 0, 10], [9, 2, 15, 10, 7, 14, 5, 0, 6, 13, 1, 3, 12, 4, 8, 16, 11]]

选择示例

本例中的选择算子采用锦标赛法进行选择。

1
2
selected = toolbox.select(pop, 3)
selected

[[16, 10, 9, 1, 2, 14, 5, 3, 7, 8, 6, 13, 0, 12, 4, 15, 11], [16, 10, 9, 1, 2, 14, 5, 3, 7, 8, 6, 13, 0, 12, 4, 15, 11], [5, 7, 6, 12, 14, 10, 11, 15, 8, 3, 1, 0, 9, 13, 4, 2, 16]]

判断个体是否被选中：

1
[ind in selected for ind in pop]

[True, True, False, False, False]

进化控制主程序

完整的主程序如下，其中算法部分直接采用了algorithms库的esSimple，即GA最基本算法控制流程。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
def main():
    random.seed(169)
    # 种群规模为300
    pop = toolbox.population(n=300)
    
    hof = tools.HallOfFame(1)
    # 设置统计变量
    stats = tools.Statistics(lambda ind: ind.fitness.values)
    stats.register("avg", np.mean)
    stats.register("std", np.std)
    stats.register("min", np.min)
    stats.register("max", np.max)
    
    pop,logbook = algorithms.eaSimple(pop, toolbox, cxpb=0.7, mutpb=0.05, ngen=40, 
                        stats=stats,verbose=False,halloffame=hof)
    
    print("最优解为：",hof[0], "目标函数值为：",hof[0].fitness.values)
    
    # 绘制收敛图
    fig = plt.figure()
    plt.plot(logbook.select("gen"), logbook.select("min"), 'r--', label="min")
    plt.plot(logbook.select("gen"), logbook.select("max"), 'b--', label="max")
    plt.plot(logbook.select("gen"), logbook.select("avg"), 'g--', label="avg")
    plt.xlabel("Gen")
    plt.ylabel("fitness")
    plt.legend()
    plt.show()
    
    # 保存图片
    plt.savefig("ga.png", dpi=400)
1
2
# 运行主程序
main()

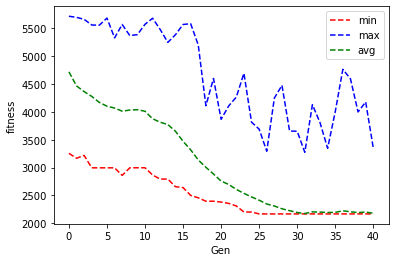
最优解为： [5, 7, 6, 0, 12, 8, 11, 15, 3, 16, 13, 14, 9, 1, 4, 10, 2] 目标函数值为： (2167.0,)

上述过程输出的收敛图如下：

收敛图